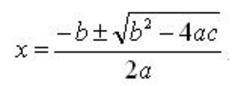Representación gráfica de funciones cuadráticas
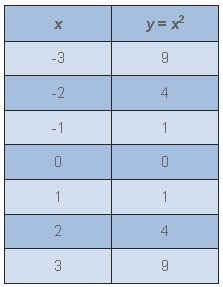
La función cuadrática más básica y simple tiene la ecuación y=x^2 . Si hacemos una tabla con los valores de esta función, vemos que el rango (los valores de y, o salida) no se comportan como una función lineal. En una función lineal, el valor de y cambia por la misma cantidad cada vez que el valor de x aumenta por 1. Eso no sucede con una función cuadrática:
Observe en la tabla que los valores de y no cambian de manera constante:
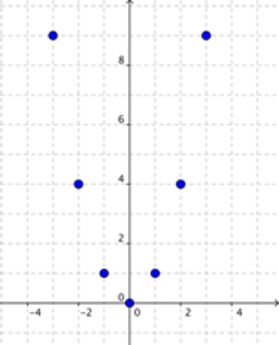
Grafiquemos algunos puntos para ver cómo se vería la función.
Después de graficar algunos puntos, podría ser tentador conectar los puntos con segmentos de línea, que son rectos. Pero esto estaría mal, y produciría un patrón que no representa la función.
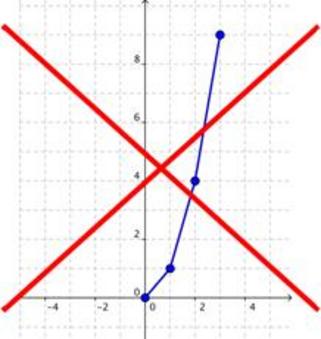
Debemos dibujar una curva suave conectando los puntos.
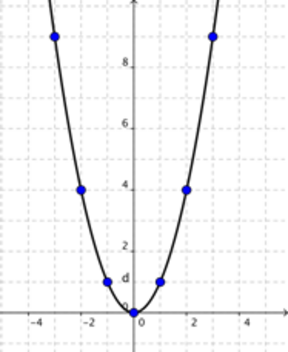
La gráfica de la parábola tiene las siguientes características:
1) Si a > 0, la parábola abre hacia arriba.
2) Si a < 0, la parábola abre hacia abajo.
3) El vértice es el punto más alto ó el más bajo de la parábola, según sea el caso.
4) El vértice se calcula con la siguiente fórmula en la cual el primer término representa la x y el segundo término representa la y.
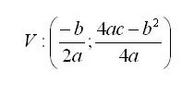
5) Si el discriminante (b2-4ac), es positivo, la parábola corta al eje x en dos puntos diferentes.
6) Si el discriminante (b^2-4ac), es negativo, la parábola no toca al eje x.
7) Si el discriminante (b^2-4ac), es igual a cero, la parábola toca al eje x en un único punto.
8) Los puntos de corte de la parábola con el eje x, son los que resultan de la resolvente cuadrática: