Ecuaciones de segundo Grado (cuadráticas)
Una ecuación de segundo grado es toda expresión de la forma:
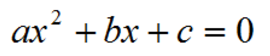
donde a ≠ 0. Ningún término en la función polinomial tiene un grado mayor que 2. Las funciones cuadráticas son útiles cuando trabajamos con áreas, y frecuentemente aparecen en problemas de movimiento que implican gravedad o aceleración.
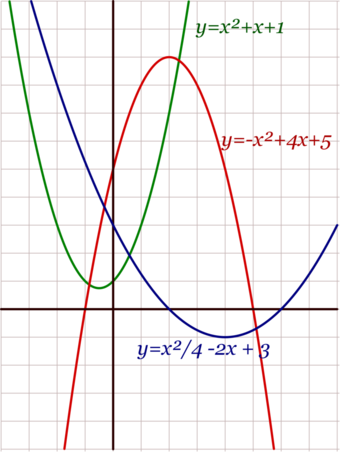
Solucionar una ecuación cuadrática es ENCONTRAR el intercepto del eje xpara esa ecuación, es decir los puntos donde la gráfica de esa ecuación corta el eje x.
Métodos de solución
Trinomio cuadrado de la forma

Características:
- Tienen un termino positivo elevado al cuadrado y con coeficiente 1
- Posee un termino que tiene la misma letra que el termino anterior pero elevada a 1 (bx) (puede ser negativo o positivo).
- Tienen un termino independiente (c) de la letra que aparece en los otros dos (puede ser negativo o positivo).
Reglas para factorizar un trinomio de esta forma:
- Se descompone el trinomio en dos factores binomios cuyo primer termino será la raíz cuadrada del termino [raíz cuadrado] .
- El signo del primer binomio será el mismo signo que tenga el termino “bx”, el signo del segundo binomio será igual a la multiplicación de los signos de “bx” y de “c”.
- Se buscan dos números cuya suma/resta sea igual que el valor absoluto del factor “b” de “bx”, y cuyo producto sea igual al valor absoluto del factor “c”, estos números son los segundos términos de los factores binomios.
Factorización
Características:
- El coeficiente del primer término es diferente de 1.
- La variable del segundo término es la misma que la del primer término pero con exponente a la mitad.
- El tercer término es independiente de la letra que aparece en el primer y segundo términos del trinomio.
Reglas para factorizar un trinomio de esta forma:
- Se multiplica y se divide el trinomio por el coeficiente del primer término.
- Se resuelve el producto del primero y tercer término dejando indicado el del segundo término.
- Se factoriza como en el caso del trinomio de la forma x2 + bx + c, o sea, se buscan dos números que multiplicados de c y sumados/restados den b
- Se factorizan los dos binomios resultantes sacándoles factor común monomio, se descompone el 15 y por último dividir.
Fórmula General
Siga los siguientes pasos:
- Ordene la expresión que le brindan igualándola a 0.
- Localice los coeficientes a, b y c.
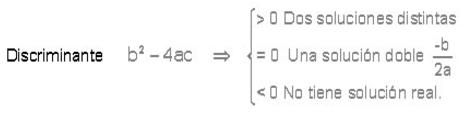
- Calcule el discriminante.
-
El DISCRIMINANTE es la esxpresión bajo el radical (radicando) cuyo resultado le permitirá predecir cómo será la solución.
Vea el video para comprender cómo se solucionan.